分治算法和汉诺塔问题

在某些实际场景中，我们之所以觉得有些问题很难解决，主要原因是该问题涉及到大量的数据，如果只需要处理少量的数据，问题会变得非常容易解决。

分治算法

比如说，需要设计一个算法对1000个整数进行排序，第一感觉是比较困难的，但同样的问题，如果转换成对2个整数进行排序，解决起来就容易多了。而之前1000个整数的问题，又可以拆解成无数个2个整数的问题，然后再组合的过程。

像这种，先将整个问题拆分成多个相互独立且数据量更少的小问题，通过逐一解决这些简单的小问题，最终找到解决整个问题的方案，就是分治算法。所谓问题间相互独立，简单理解就是每个问题都可以单独处理，不存在“谁先处理，谁后处理”的次序问题。

分治算法解决的经典问题有很多，包括汉诺塔问题，以及后面要讲到的二分查找算法、归并排序算法、快速排序算法等。本节先介绍典型的汉诺塔问题。

汉诺塔问题

汉诺塔问题，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。64根柱子移动完毕之日，就是世界毁灭之时。

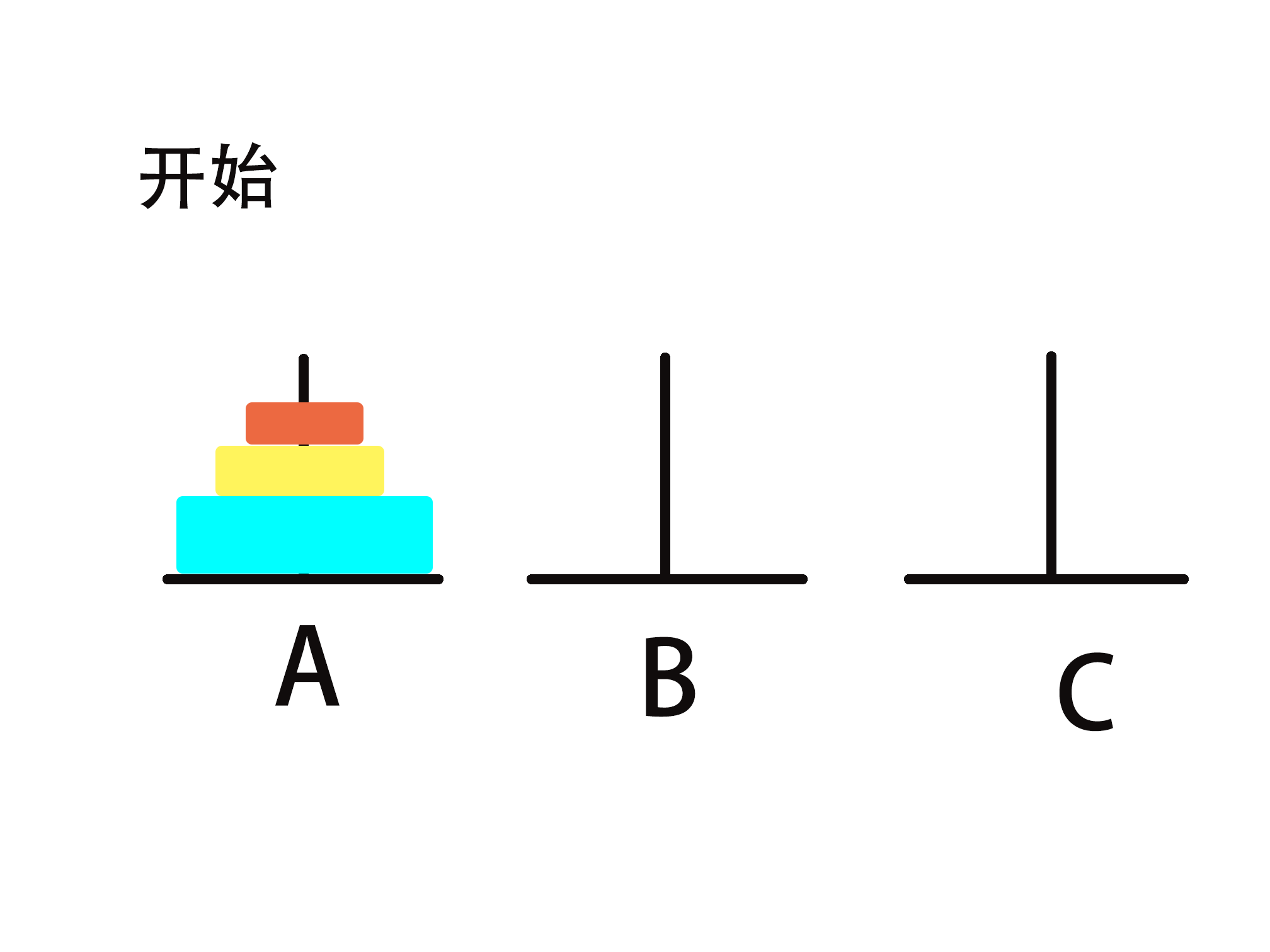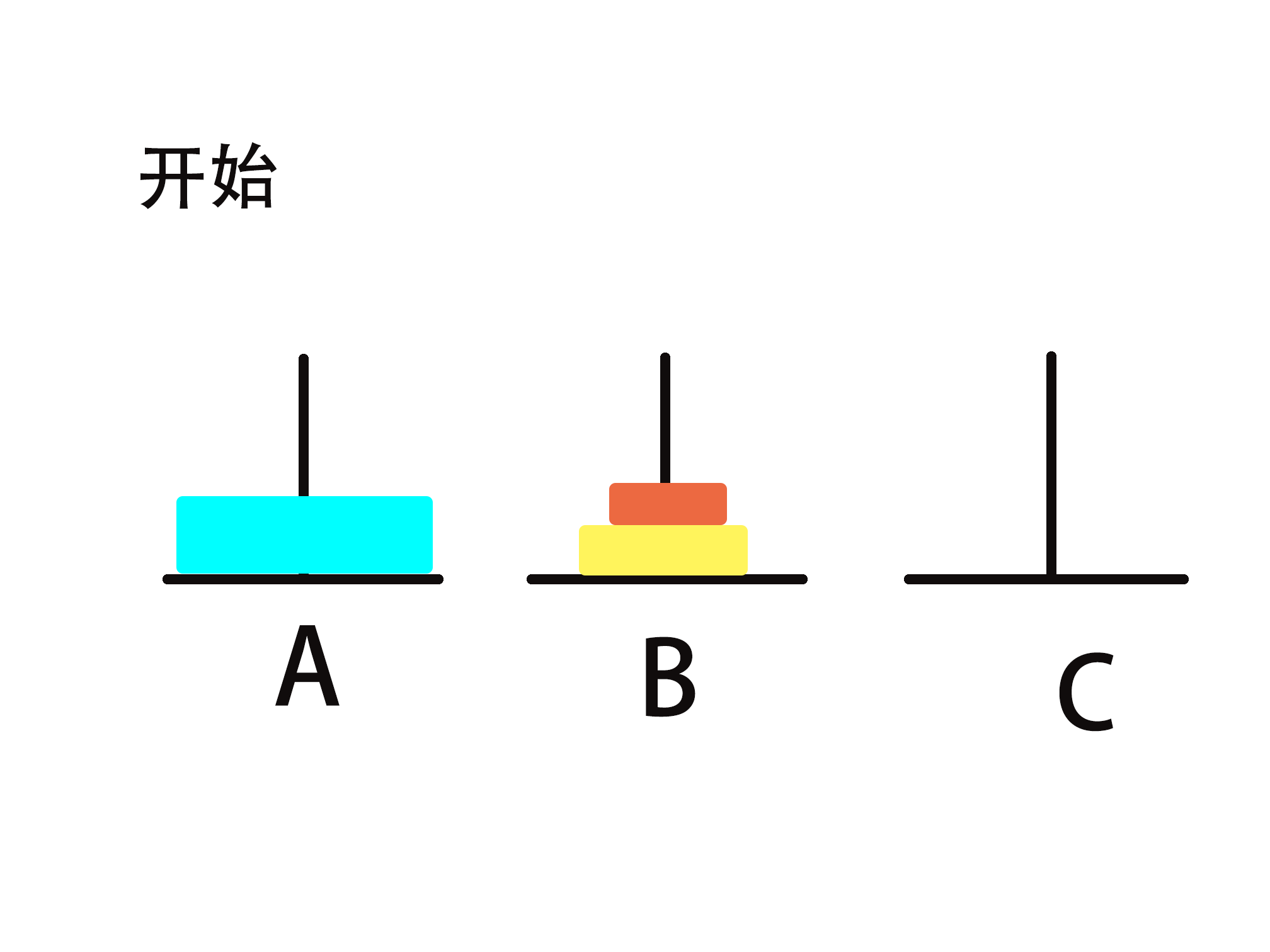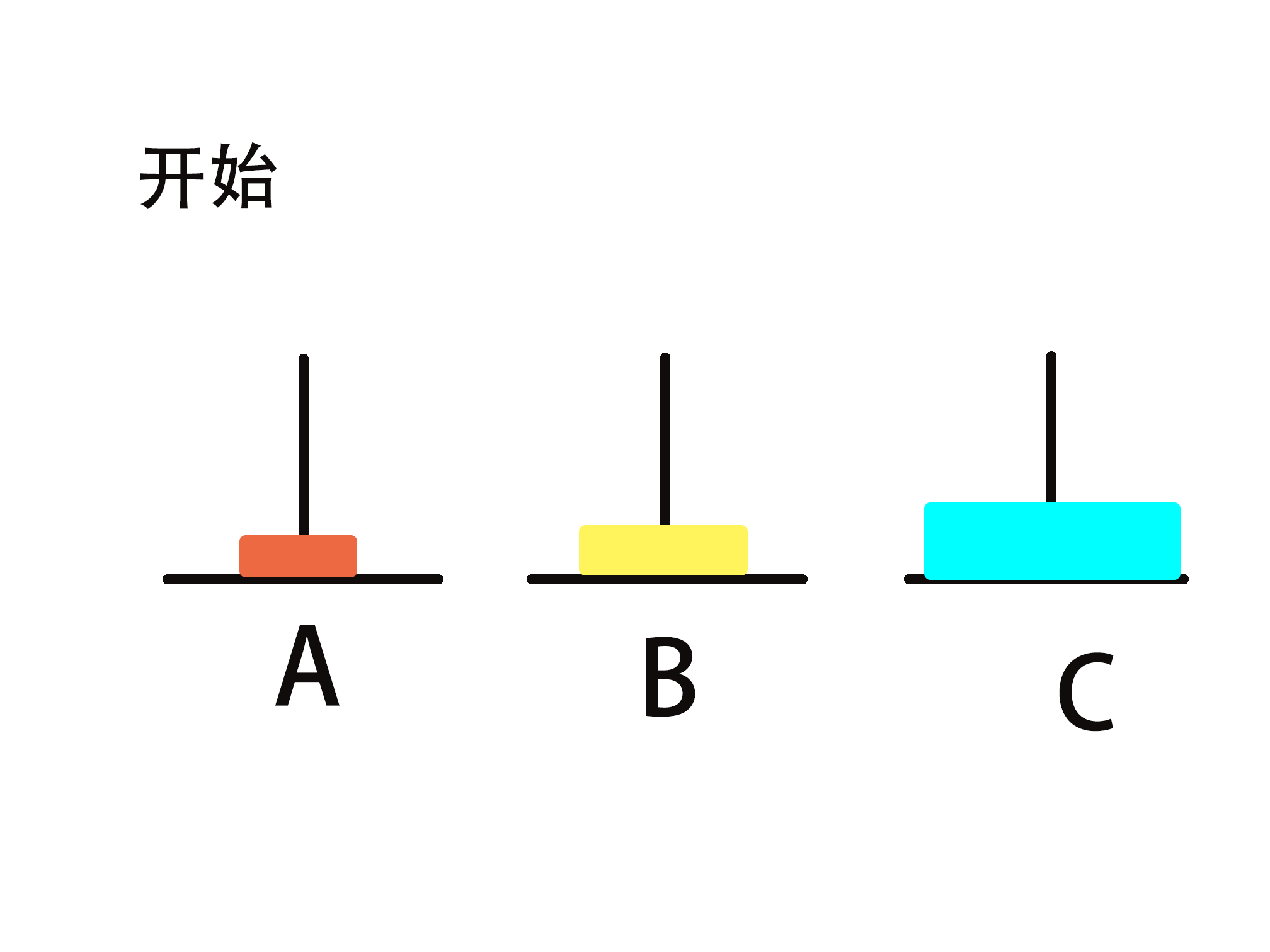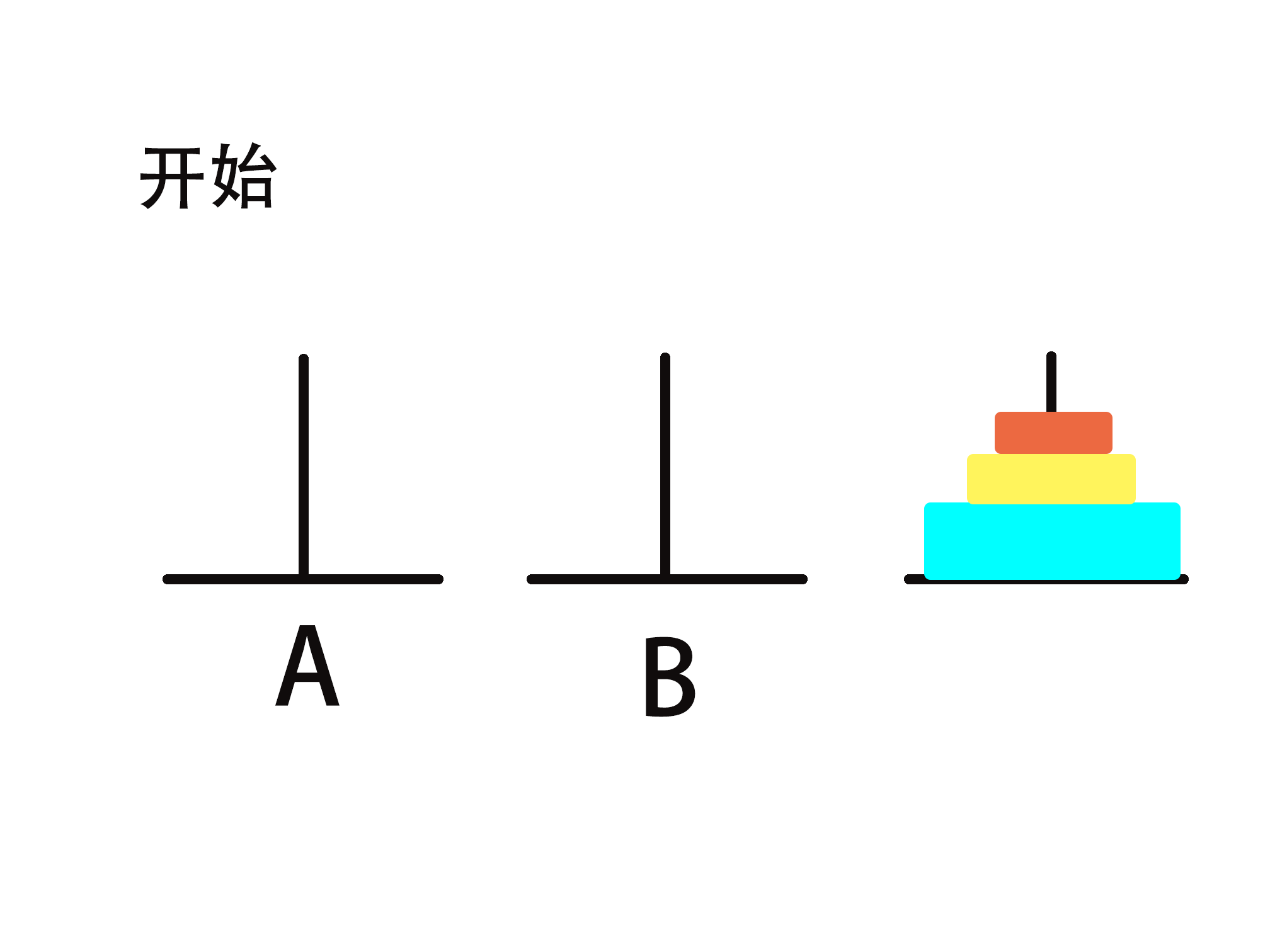
分治步骤拆解

1) 把n-1个圆盘从A经过C移动到B

2) 把第n个圆盘从A移动到C

3) 把n-1个小圆盘从B经过A移动到C

代码实现

def hanoi(n, a, b, c):
    if n>0:
        hanoi(n-1, a, c, b)
        print('moving from %s to %s'%(a, c))
        hanoi(n-1, b, a, c)

hanoi(3, 'A', 'B', 'C')

移动次数

1) 汉诺塔移动次数递推式：h(n) = 2h(n-1)+1

2) h(64) = 18446744073709551615

3) 假如婆罗门每秒钟搬一个盘子，则总共需要5800亿年。