前面文章中,我们用数学推导的方式,求解了线性回归问题,但直接求解计算量很大,特别是矩阵求逆的过程。在机器学习中,人们更倾向于用一种近似的方式,去拟合线性规律,那就是梯度下降法。
梯度下降法(Gradient Descent, GD),常用于求解无约束情况下凸函数(Convex Function)的极小值,是一种迭代类型的算法,因为凸函数只有一个极值点,故求解出来的极小值点就是函数的最小值点。
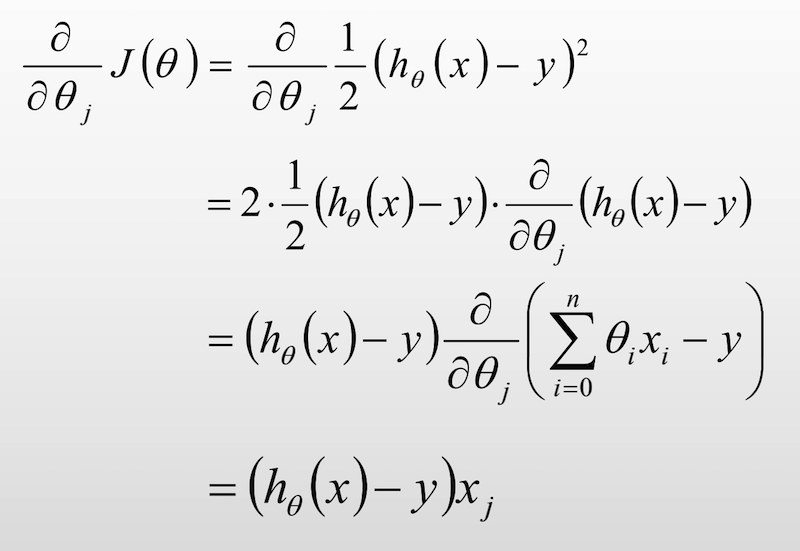
代码示例
1、创建数据集和目标函数
from matplotlib import pyplot as plt
import numpy as np
X = np.linspace(-1, 1, 100)
y = 5 * X + 3
# plt.scatter(X, y)
# plt.show()
def func(x, a, b):
return a * x + b
2、计算BGD,并更新参数
a = 0
b = 0
lr = 0.05
a_sum = 0
b_sum = 0
for i, x in enumerate(X):
a_sum += (func(x, a, b) - y[i]) * x
b_sum += func(x, a, b) - y[i]
a -= lr * a_sum/len(X)
b -= lr * b_sum/len(X)
print(a)
print(b)
3、迭代更新
迭代停止条件:迭代10000次,或者损失误差变化小于10e-10
loss = 0
for step in range(10000):
......
# 计算最新损失值
loss_cur = (func(x, a, b) - y[i])**2
if abs(loss_cur - loss) < 10e-10:
break
else:
loss = loss_cur
if step % 100 == 0:
print('step:', step, 'loss:', loss_cur, 'a:', a, 'b:', b)
4、可视化展示
y_hat = a * X + b plt.plot(X, y_hat, c='r') plt.scatter(X, y) plt.show()
本文为 陈华 原创,欢迎转载,但请注明出处:http://ichenhua.cn/read/252



